Among the many continuous probability distributions used in statistics, the Gamma Distribution stands out for its flexibility in modeling various real-world phenomena. It is especially useful when studying the time until multiple events occur, such as the total lifetime of several components or the total waiting time for several customer arrivals. Because of its versatility, the Gamma Distribution plays a major role in engineering, risk assessment, and process reliability.
What Is the Gamma Distribution?
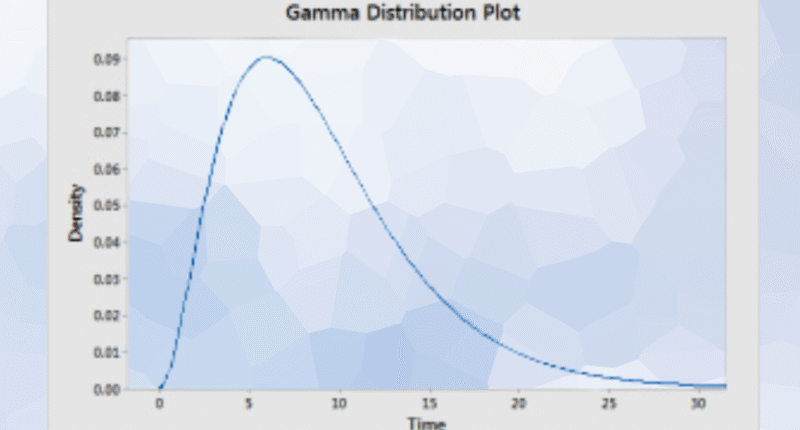
The Gamma Distribution describes continuous data that represent the waiting time until a certain number of events occur in a process that happens randomly but at a steady rate. It can take on many shapes depending on the data, making it suitable for different types of time-based or lifetime analysis.
In simple terms, while the Exponential Distribution models the time until the first event happens, the Gamma Distribution extends that idea to model the time until multiple events occur. This makes it an essential tool for systems or processes involving multiple stages or components.
Why the Gamma Distribution Is Important
The Gamma Distribution is valuable because it can model a wide range of real-world data patterns — from highly skewed to nearly symmetric. It is particularly used for:
- Predicting the total time before system failure when multiple components work together.
- Modeling waiting times or service durations in queueing systems.
- Analyzing rainfall amounts, insurance claims, or other naturally varying phenomena.
Its flexibility allows it to describe processes that are not constant over time, unlike the exponential distribution, which assumes a constant event rate.
Real-Life Example: Reliability Testing of Machine Components
Consider a factory testing the reliability of a new machine composed of several critical parts. Each component has a random lifetime before it fails. The Gamma Distribution can model the total operational time of the machine until all parts have failed or until a certain number of failures have occurred.
For instance, if a machine’s three key parts fail independently at random times, the Gamma Distribution helps estimate how long the system can operate before experiencing three total failures. Engineers use this information to:
- Plan maintenance intervals more effectively.
- Improve design reliability by analyzing failure patterns.
- Estimate product warranties and costs.
This example demonstrates how the Gamma Distribution supports predictive maintenance and quality improvement in manufacturing environments.
Applications Across Industries
The Gamma Distribution is used across diverse fields, including:
- Reliability Engineering: Estimating total system lifetime or time to failure.
- Finance: Modeling claim amounts and aggregated risks in insurance.
- Hydrology: Predicting rainfall intensity or river flow variability.
- Healthcare: Analyzing waiting times for patient recovery or hospital arrivals.
Its ability to adapt to different shapes and rates of variation makes it one of the most powerful tools in statistical modeling.
Conclusion
The Gamma Distribution is a highly flexible continuous probability model that extends the idea of waiting time analysis to multiple events. Its applications in reliability, engineering, and risk management make it indispensable for understanding how time-dependent processes behave. By using the Gamma Distribution, analysts and engineers can make informed decisions that improve system performance, reliability, and overall operational efficiency.