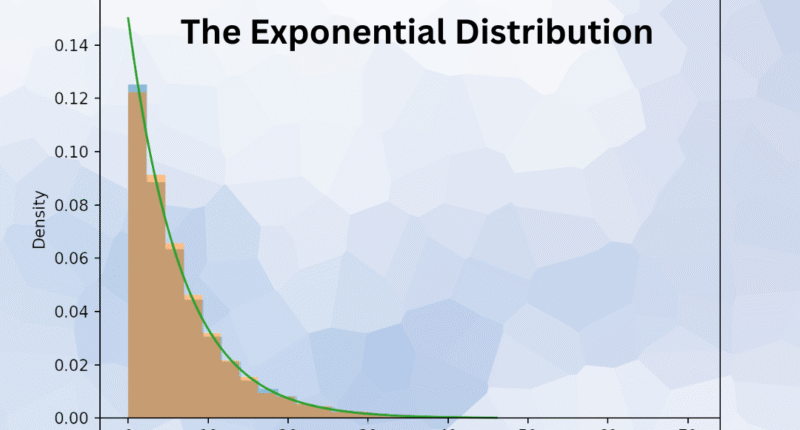
The Exponential Distribution is one of the most widely used continuous probability distributions in statistics and reliability engineering. It is particularly useful for modeling the time between events in a process that happens continuously and independently at a constant average rate. In simple terms, it helps describe how long you might wait until the next event occurs — whether that event is a machine failure, a customer arrival, or a phone call.
What Is the Exponential Distribution?
The Exponential Distribution represents the likelihood of an event occurring over time. It is often associated with systems or processes where events happen randomly but with a consistent average frequency. Unlike the Normal Distribution, which is symmetric, the exponential distribution is skewed to the right, meaning most events occur relatively quickly, while a few take much longer.
This distribution is often used to model:
- The time until a machine breaks down
- The waiting time between arrivals at a service counter
- The lifetime of electronic components
Why the Exponential Distribution Is Important
The exponential distribution provides a simple yet powerful way to analyze time-dependent events. It helps predict how long systems can run before failure and is fundamental in reliability engineering and quality management.
Key characteristics include:
- The probability of failure or event occurrence remains constant over time.
- It effectively models random processes with a steady rate of occurrence.
- It provides insights into system reliability and service efficiency.
Because of these features, it is frequently applied in manufacturing, healthcare, logistics, and customer service industries.
Real-Life Example: Machine Failure Analysis
Imagine a factory where machines occasionally stop working due to component wear. Suppose that, on average, a machine fails once every 100 hours of operation. The Exponential Distribution can describe the probability that a machine will fail within the next 50 hours, or how likely it is to continue running longer than 200 hours.
This understanding allows engineers to:
- Plan preventive maintenance schedules
- Estimate warranty periods
- Predict equipment reliability
By applying the exponential model, manufacturers can minimize unexpected downtime and optimize maintenance efficiency.
Applications Across Industries
The Exponential Distribution has wide-ranging applications, such as:
- Telecommunications: Modeling the time between incoming calls.
- Healthcare: Predicting the time until patient arrivals in emergency departments.
- Banking and Retail: Estimating customer waiting times in queues.
- Reliability Engineering: Evaluating system performance and failure patterns.
Its simplicity and versatility make it a fundamental tool in operational decision-making and process improvement.
Conclusion
The Exponential Distribution is a cornerstone of continuous probability models, providing valuable insight into how events unfold over time. Whether predicting equipment lifetimes, customer arrivals, or service delays, it helps organizations understand and manage uncertainty effectively. By leveraging this distribution, businesses can improve reliability, reduce downtime, and make smarter, data-driven decisions in time-dependent processes.